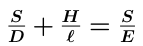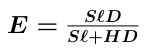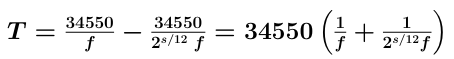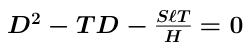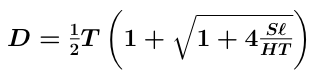Physics of Musical Instruments
Table of Contents
1. Any pipe makes a simple musical instrument
The simplest type of musical instrument capable of producing a sustained note is a length of pipe. If you blow across the end of a pipe, you hear a note resonating from it. This note is always the same no matter what you are doing to produce it; I can play it like a trumpet, or strike it with my hand or some other flat object, and I hear the same note. It is clear that the pipe itself wants to sing that note, and I am merely giving it the energy it needs to do so. What is it that makes a pipe pick out a particular note that it wants to play?
Take three or four soda straws, cut them to different lengths, and blow across the tops of them to hear what note they play. What do you notice about how the length of the straw relates to the note played? It should be the case that the shorter the straw is, the higher the note that it wants to sing. We're going to try to figure out what’s going on when a pipe “sings” a particular note.
For this next demonstration I’m going to use a length of pipe standing in a graduated cylinder full of water. Since it's a bit hard to see how blowing over a pipe produces sound, I'll instead use a tuning fork, a fork-shaped piece of metal made so that it vibrates at a particular, known pitch. To get it to vibrate, I just hit it against something fairly soft, like the rubber sole of my sneakers. It’s not at all loud; in fact, it’s probably not even audible at the other side of the room. However, we can use it to make the pipe sing a note that you all can hear.
Here’s what I’m going to do. I’ll hold the vibrating tuning fork over the pipe and gradually slid the pipe up out of the water. As we deduced from the experiment with the straws, as I change the length of the column of air in the pipe by lifting more and more of it out of the water, the note that that pipe sings will change. Now suddenly, when I get to the correct length, the pipe is singing back to us, a clear and quite loud note that some of you may be able to tell is the same note as that produced by the tuning fork. If I raise or lower the pipe by even a quarter of an inch, it no longer sings. Blowing over the top of the pipe produces the same note again that you heard it singing.
What’s going on here? Let’s talk a bit, first, about what sound is made out of; then we’ll be better equipped to explain why a tube produces a particular sound.2. Sound is made out of compressions moving through air
You're probably familiar already with the idea that sound is made out of some sort of "waves" traveling through the air, because you have heard phrases like "sound waves" and "the speed of sound.'' But what exactly is sound "made" of, and how does it move through the air?
If I clap my hands, everyone in the room can hear it. It is clear that clapping produces sound, and that that sound somehow travels through the air and into your ears. But what exactly did I do to the air to create this sound? If you watch as I clap in slow motion, and try to imagine what the air around my hands is doing as I clap, you'll realize that for most of the time that my hands are moving, the air doesn't have to move much to get out of the way, but just as my hands hit each other, there's still a bit of air between them that has to move really quickly to get out in time, in the same way that someone waiting at the bus stop can walk slowly onto the bus while someone who is a far distance away has to run to get there before the bus closes its doors and moves on. If you make a pocket of air with your hands and then quickly squeeze them together, you hear the air hissing out; it has to do the same thing even faster when you clap.
Thunder gives us another good example of sound traveling through air. When lightning strikes, it heats up the air around it, and that air expands, leaving an empty space in the air right along the line of the lightning. A fraction of a second later, the surrounding air rushes in to fill in that space, and all slams together in the middle. Thus, the word "thunderclap" really is a good description of it; the air is doing the same thing that my hands are doing when I clap.
What is happening in both these examples is that air is forced out of one place and pushes at the air around it, forcing it further out. You can see the same sort of thing happening if you hold the end of a slinky in you hand, letting the rest of it hang downwards (but not touch the floor), and then you use your other hand to tap the hand holding the slinky. This tiny tap on your hand travels as a visible disturbance down the slinky, and you can hear a click as it knocks the last few loops of the slinky against each other. The same sort of thing happens in a ballpark when someone decides to start a "wave:" when people next to them see them stand up and wave, they do the same thing, and although each person doesn't move very far, the wave gradually travels all around the stadium. Or, if you throw a rock into a pond, the water the rock pushes our of the way pushes and pulls on the water around it to form a ripple that spreads out around the pond. In air, clapping or thunder produces an expanding sphere of air that is packed together more tightly than the air around it; we call this a "compression." Eventually this compression in the air will hit your eardrum and push it inward, causing you to hear a sound. Now you can understand why fireworks are so loud - an explosion is just a lot of air moving very quickly out of a certain spot, and thus makes a very big compression traveling through the air.
The first person we know of who came up with the idea that sound was a vibration moving through the air was Pythagoras, a Greek philosopher and mathematician who you might have heard about because of a theorem he came up with having to do with triangles. Pythagoras lived in the sixth century BC.3. Echoes are sound bouncing off of solid obstacles
You probably know that sound bounces off of things like buildings and mountains - this is called an "echo". If you shout at a mountain, you may hear it shout the same thing back a few seconds later. In a more common experience, if you're outside hammering on something, you may think that you hear someone else across the street hammering as well, a fraction of a second later than you. This is the sound wave from your hammering bouncing off of the building on the other side of the street. If you listen carefully, you might even hear a third echo, when that echo bounces off your building, then off the other side of the street again, and then coming back to you. Unfortunately, this is easiest to hear early in the morning or late at night when there aren't many cars on the street, which is just when your neighbors won't appreciate the hammering!
Thunder also gets reflected off of different obstacles. You may have noticed that when lightning strikes right near you, it sounds like a single enormous "Crack!," whereas in the distance it sounds like a long rumble. Now, if you were right next to that lightning bolt in the distance, it would sound like a single clap; what makes it into a rumble in the distance? The reason is that it is bouncing off of all the hills around you, and what you really hear is a whole jumble of echoes arriving one right after the other.
You can see echoes also in the surface of a pond when you have dropped a rock into it; when the ripples hit a rock or log in the pond, new ripples spread back out in all directions from that obstacle. A waterbug standing right near where the rock hit will feel one big ripple, but one far away will feel a jumble of little ripples bounced off all the various obstacles; this is the same as how the lightning sounds like a single sound when heard from nearby but sounds like a rumble from a distance.
If you stand in a large empty hallway or room, close your eyes, and clap, your brain can imagine what the shape of the room must be simply from how long it takes the sound to echo back from the walls in each direction. If you're walking around in the dark, you can tell that there's a wall near you when the room sounds "dead" in that direction; this happens because the echoes from that wall are so close behind the sound of your footsteps or of echoes from the rest of the room, that your brain can't tell that any sound at all is coming from that direction. Bats use a much more effective form of this "echolocation" that allows them to locate even tiny insects by echo. Your brain figures out what direction a sound comes from by analyzing how the sound reflects off of the various curved surfaces of your ear.4. Sound travels at a specific speed
We might think that sound would travel faster if it was louder. After all, the air around an exploding firework is trying to escape much more urgently that the air between my hands when I clap; it seems like the resulting sound wave would travel a lot faster. The air at a distance from whatever produced the sound doesn't know how urgently the air near the sound was trying to get away; all it knows is that it's being pushed, and it will respond in its own time. The ballpark wave shows this same phenomenon. Each person sees the person next to them start to move and takes a specific amount of time to stand up and sit back down. Therefore, the speed the wave travels at is determined by how quickly individual people tend to respond, not by how enthusiastic the people who started the wave are. Similarly, you may notice that ripples in a pond move at the same speed no matter how big they are.
You've probably heard people talking about "the speed of sound." We measure the speed of some of our faster airplanes by how much faster than sound they travel; a jet traveling at Mach two is moving twice as fast as sound. The fact is that all sound in air does travel at exactly the same speed, a speed that becomes only slightly slower at higher altitude and lower temperature. At sea level and room temperature, sound travels at about 761 miles per hour. This means that a sound travels about a mile every five seconds. If you see lightning in the distance and count how many seconds it takes the sound of the thunder to reach you, you can divide that number of seconds by five to get an estimate of how many miles away that lightning strike was. In physics, we prefer to use metric units when we can, so we say that the speed of sound is 345 meters per second.5. A musical note is a continuous wave of sound
All of the sounds that we've talked about so far, such as clapping, hammering, and lightning, are a single, sharp noise that happens once. Much of the sound that we hear, like my voice or the honk of a car horn, is of a different sort; it is a continuous sound of a definite pitch, rather than a sudden sound with no easy-to-hear pitch. A constant pitch of sound is produced by compressions that are spaced out evenly, like the ripples spreading on a pond.
A simple experiment you might do to see how this works is to take a long flat piece of springy metal, like a hacksaw blade, and clamp one end of it to a table, letting the other end hang out into the air. When you pluck the end of the blade, it wobbles up and down about once per second. Now loosen the clamp, slide the blade in a bit toward the table, and clamp it again. When you pluck this shorter blade, it wobbles more quickly. If we shorten it again, to about four inches long, it is vibrating to fast for us to track with our eyes, and it is starting to make a sound, a really low buzing noise. As we shorten it more, this noise gets higher in pitch and louder, and it always sounds like mostly one continuous note.
So, we've discovered a way to produce a musical note, and we know how it was generated: the hacksaw blade is vibrating back and forth, faster than we can see, pushing out a wave of compressed air every time that it gets to one end of its swing. All of the sounds that we hear that are a single continuous note are this sort of continuous wave.
The pitch of a note is determined by how fast the thing creating it is vibrating. Pitch is typically measured in vibrations per second, or Hertz (Hz). Middle C on a piano is 278 Hz; the lowest a human can hear is about 20 Hz and the highest is about 20,000 Hz. That's an impressive range, but some animals are even better; whales and elephants communicate using rumbles that are too low for human hearing, and bats can hear (and squeak) at 150,000 Hz.6. Sound waves can interfere constructively or destructively
If you were to watch a small bit of air as a note is being played, you would see that bit of air (and all the others around it) swinging back and forth in time with the note. Just as in a ballpark wave or a ripple in a pond, the individual pieces of the "medium" that the waves is travelling through don't really go far from their starting point; the wave is carried by all those pieces moving back and forth at the right time.
Now, we can think about these mving bits of air as if they were like a person swinging on a swing. If a person is just sitting on a swing that is going back and forth, he will stop moving soon. It's the same with sound waves in air; when nothing is forcing the air to vibrate, those vibrations quickly die out. When there is some object vibrating, like a hacksaw blade or guitar string, it keeps pushing on the air near it to keep it moving back and forth.
Now, you may realize, from experience with pushing a young child on a swing, that timing is key. If you push them forward each time they get back to the end of a swing, they will swing higher and higher. However, if you were to push them backwards as they were swinging forward, it would stop them, or at least slow them down. The same thing happens with sound waves. The hacksaw blade keeps the air vibrating because it pushes on the air again every time that it swings back toward the blade. If you push at the wrong time, the air stops moving; it is being pulled two ways at once and goes neither way. Some high-tech earphones work this way, recording the sound waves from the air outside your ear using a tiny microphone and then moving a tiny speaker to push backward on the air when it's moving forward and forward when it's moving back.
Another good example of this is the way that there are so-called "dead zones" in a room when music is being played - spots where the musics can't be heard as well, or doesn't sound as full as it's supposed to. I've set up two speakers to both play the same note. if you move your head back and forth (it helps if you cover one ear as well), you'll notice that in some spots, the sound is quite loud, while in others, it can hardly be heard. What's happening here is that in some locations, the sound waves from both speakers are arriving at the same time, while in other locations, one speaker is further away and, as a result, the peak of the sound wave from that speaker is arriving just as the trough from th other is, and they cancel out.
The same thing is happening inside of the tube in a graduated cylinder that we looked at way back at the start. Each sound waves sent out by the tuning fork is reflecting off of the bottom of the cylinder and coming back up to the top. Now, if it gets there just at the same time that a new wave is coming in, the new wave is pushing just at the right time to reinforce the one already in the tube, just like you pushing at the right time to make the child swing higher. But if the tube is just a little bit too long, the wave will get back to the entrance of the tube at the wong time to be pushed on by the new wave, and the air inside of the tube will just all be a muddle not knowing what way to go. This phenomenon where an object responds to a vibration at a certain frequency by beginning to vibrate itself is called "resonance."7. Musical Notes and Scales
Let's go back to the straws we were using before, and do a specific experiment with them. Take one straw, and cut it exactly in half. Try blowing over the top of the half-straw, then a full straw. Do you notice something special about the relationship between those two notes? If you know a bit about music, you might realize that the note from the half straw is one "octave" above that from the full straw. Now, try plugging the bottom of the shorter straw with your finger, and blowing over the top of it. Is the note lower, higher, or the same? Now compare it to the note from the full straw. What do you notice?
The octave is an important interval in music because two notes an octave apart “sound good” together. The ancient Greeks came up with a really interesting explanation for why notes sound good together: they decided that how “good” two notes sound together is can be determined by how “simple” the ratio of their lengths is. An octave, they reasoned, is a very pleasant interval because it comes from pipes with a length ratio of 1/2, which, of all fractions, has the smallest sum when the numerator and denominator are added.
Try this out yourself. Think up the “simplest” fractions that you can find between 1/2 and 1, and cut that fraction of the full straw; then see how it and the full straw sound when played together. If you know music theory, you may even be able to build a full scale of notes just using your straws. Can you find three straws that still sound good when played together? How about four? Can you find two straws that you think sound absolutely awful together?
This process that you just did is the way that the musical scale was first built. The chart below lists the intervals in music theory, and what the ideal ratio for them is. In modern times, this ideal scale was replaced with one in which the ratio between any two notes that are a half step apart is exactly the same; the ratios in this system are also shown.
| Interval | Ratio (ideal) | Ratio (equal) |
|---|
| Unison | 1 | 1 |
| Minor Second | 25/24 | 1.059 |
| Major Second | 9/8 | 1.122 |
| Minor Third | 6/5 | 1.189 |
| Major Third | 5/4 | 1.260 |
| Perfect Fourth | 4/3 | 1.335 |
| Tritone | 25/18 | 1.414 |
| Perfect Fifth | 3/2 | 1.498 |
| Minor Sixth | 8/5 | 1.587 |
| Major Sixth | 5/3 | 1.682 |
| Minor Seventh | 16/9 | 1.782 |
| Major Seventh | 48/25 | 1.888 |
| Octave | 2 | 2 |
In western music, the two notes that are generally considered to sound worst together are those whose straws have a ratio equal to the square root of two. This interval is called the "tritone," and was considered in the middle ages to be "the devil's interval." Accidentally including it in a piece of music that you were writing would put you in danger of being burned at the stake, in some places and times. Now we know that this interval is jarring simply because it is not a rational number at all, and some sirens use it in order to be more noticeable.
This requirement that the sound travel two lengths of the pipe in the time it takes for the tuning fork to vibrate once gives us a way to relate pipe length to frequency. If I want a pipe that plays an A-440 (that is, the note at 440 Hz, which happens to be an A), sound waves have to go around it once in 1/440 second. So, (2 x (length of pipe in m)) / (345 m / s) = (1 / 440) s. We can solve this equation algebraically to find that the length of pipe must be .392 m (39.2 cm). Below is a table showing the frequencies of some notes and the length of straw that plays that frequency:
| Note | Frequency (Hz) | Length (cm) |
|---|
| A | 440.00 | 19.6 |
| A# | 466.16 | 18.5 |
| B | 493.88 | 17.5 |
| C | 523.25 | 16.5 |
| C# | 554.37 | 15.6 |
| D | 587.55 | 14.7 |
| D# | 622.25 | 13.9 |
| E | 659.26 | 13.1 |
| F | 698.46 | 12.3 |
| F# | 739.99 | 11.7 |
| G | 783.99 | 11.0 |
| G# | 830.61 | 10.4 |
| A | 880.00 | 9.8 |
The notes C, D, E, and F, highlighted above, are the first five notes of the C scale. Let's cut our straws to these lengths and see if we can play some familiar songs on them. With a large number of people, you can have each person pick a particular note and play that note when called upon to do so. If you're doing this yourself, you can cut the five lengths and hold them spread out in your hand so that you can blow on any of them. Below are the notes to some songs; I'll count on you to know the rhythm.
Mary had a little lamb:
E D C D E E E D D D E G G
E D C D E E E E D D E D C
Ode to joy:
E E F G G F E D C C D E E D D
E E F G G F E D C C D E D C C
D D E C D E F E C D E F E D C D (G)
E E F G G F E D C C D E D C C
Here, the (G) represents a G that is one octave lower. Do you remember how to get a straw to play one octave lower? Be ready to cover the far end of your G straw with a finger when you get to that point.8. A mouthpiece produces vibration
The straws that we have now are a useful instrument, but nowhere near as loud as a flute or clarinet. What is it that makes these more complex instruments able to make so much more noise when you blow through them?
The key part here is the mouthpiece. The mouthpiece of a wind instrument is designed to make a vibration that will resonate in the bore of the instrument (the cylindrical cavity inside). Mouthpieces work by letting a blast of air into the instrument, then suddenly shutting of the enetrance, then opening it and letting another blast in, all in a cycle that takes place as quickly as the vibration of the note being played. In clarinets, oboes, and other reed instruments, this is accomplished by a reed that swings back and forth like a vibrating hacksaw blade, alternately covering and opening the instrument's opening.
You can create an oboe-like reed on a straw by cutting the end of a straw into a triangle shape, thus creating two triangles that touch each other whn the straw is pinched. If you press the "reeds" together with your lips and blow, you may be able to get the mouthpiece to buzz. However, this is really hard to play. Let's try something a little harder to make and a little easier to play.
For this second mouthpiece, cut out a square from the top of a straw right near the end. Now, if you blow through the straw, you should hear a whistle at the not that straw normally plays. To make it louder and clearer, wad up some paper and pack it into the straw so that there is only a thin channel that air can get through, and that channel of air hits the hole you just made.
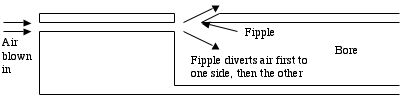
A hole like this is called a "fipple." A picture of what it looks like on a real whistle is shown below. As the jet of air from the channel hits the sharp edge on the far end of the hole, it may be deflected up slightly. If so, this will draw air out of the instrument's bore as well, reducing the pressure there. This creates a vacuum effect that pulls the airstream down into the bore. Then, this air blowing into the instrument eventually creates a high pressure inside the instrument that forces the airstream back out. This whole cycle is happening hundreds of times a seconds, in time with the vibration of the air in the tube.
In my whistles, I typically make the fipple hole by drilling a round hole of about 7/32'' (same size as my finger holes), then cutting it out with a skill knife to be a rectangle a bit wider than it is long. Then, I shave down the far side into a blade shape. The block for the mouthpiece is simply a piece of dowel with a channel carved out of one side, which I make by just cutting a chord across the circle. The channel should be fairly small in order to properly focus the air on the fipple. You get better tone if the channel is perfectly straight (although it's easier to play if you make it a bit bigger near where you put your mouth, thus focusing a more powerful stream of air on the fipple). You get a clearer tone if the channel is very smooth.
9. Finger holes make it easier to play many notes
The straws that you've been using so far would work great as a "pan-pipe," organ, or some other instrument for which there is one tube for each note. However, most instruments work by opening and closing finger holes to change the note being played. Can we figure out mathematically how holes ought to be placed to play the note we want?
In order to do this, we need to introduce the idea of "acoustic length." In order to figure out what note a flute will play, we need to take into account the effects of the mouthpiece, and the lesser effect of the shape of the "bell," the end of the instrument. We can figure out, by measuring the tone that the flute plays, how long a tube it thinks it is; this is its "acoustic length." We will find that the pipe thinks itself a bit longer than it is; there is an "end correction" of .3 times the diameter at the open end, accounting for the time it takes for the air going through the instrument to realize that it is no longer confined by walls, and there is some mouthpiece correction that is hard to determine theoretically but which can be found by subtracting the end correction and the pipe length from the acoustic length determined experimentally.
We now want to figure out the acoustic length of our flute with one hole on the side, which will tell us what note it plays. In order to do this, we will introduce the idea of "admittance." The admittance of a pipe is a number telling us how easily air flows through it. For a cylindrical pipe which has a cross-sectional area A and a length l, the admittance is A / l. In other words, the longer the pipe, the harder it is to blow through it, and the wider the pipe, the easier it is to blow through it. If we can find the admittance of our pipe-with-hole arrangement, then figure out what length of the basic pipe would have this same admittance, we will have found the acoustic length of our pipe-with-hole.
We can view this as two pipes being joined together. The admittance of the combination is just the sum of the admittances of the individual pipes. This is what we would expect, since air can travel one of two ways from there. We can use this to figure out the total admittance, and hence the equivalent acoustic length of pipe, of our flute with one hole in it.
The main bore, beyond the hole, has an acoustic length of l = d+.3b, where b is the diameter of the bore and d is the distance from the hole to the end of the pipe. To get the acoustic length, we need to add .3b to the pipe length simply because it takes a bit of time for our air stream to realize that it is free of the pipe. This is called an "end correction." The cross-sectional area of the bore is S = ? b2 / 4. The hole has an area of H = ? a2 / 4 and an acoustic length of l = t+.75a, where t is the thickness of the wall and a is the diameter of the hole. The end correction for a side hole is .75a.
The .3 and .75 for the end corrections are sort of "magic" numbers that you'll have to accept as true for now; there's a lot of complex fluid dynamics involved in deriving them. When I made my first PVC pipe whistle, I could not find anywhere in my textbook a value for the hole end correction. I first tried .3, and got somethign that sounded completely off. Then, I tried to derive what the value should be by finding the pitch of the note played with the first hole open and working backwards; this worked better, but still sounded out of tune. Finally, I found a footnote in a 1960 paper by A. H. Benade (one of the most famous people in this field, although he was really a nuclear physicist who dabbled in music on the side) that said "The author typically uses the value .75 for this constant." "That's my number!" I shouted, as I ran downstairs to drill what would now be the third set of holes in my whistle (The others I patched with duct tape, but the top of the whistle was now so riddled with holes that I had to drill the correct holes off to the side, which gives me an odd canted appearance when I'm playing that particular whistle).
We now know the admittance of both branches. We can ask the question, "What length E of the original pipe would have the same admittance?"
This can be solved algebraically to yield:
This means that if we were to view the pipe as having been simply cut off where the hole is, E is the necessary end correction.
Sadly, this only tells us how to figure out what note a pipe will play with a given hole. In order to figure out where to drill a hole to get the right note, we need to somehow work backwards. The math gets much worse from here on in, as we try to figure out the hole positions.
We know the frequency f of our undrilled pipe, from having played it and matching that note to a piano or computer. We know how many half steps s we want to go up from this to get to the next note; thus we know the frequency of the next note. This allows us to figure out how much we need to shorten the acoustic length by in order to get the correct note. We will call this length T:
Looking at the picture above, it is clear that T = D - E. We can substitute in our expression for E, and try to solve for D:
This can be solved by the quadratic formula:
The distance at which we should drill the hole, of course, is just this minus the end correction that we had previously found. The new end correction is E = D - T. We are now back to the situation we were in before; we can draw the pipe as cutting off where we just put the hole, with the end corection E that we just found, and it is clear that we can repeat the process to make the next hole.
If you'd rather not have to do the calculations yourself, you can use the hole calculator here.